1. ЦЕЛИ И ЗАДАЧИ ВЫПОЛНЕНИЯ КОНТРОЛЬНО - КУРСОВОЙ РАБОТЫ

Выполнение контрольно-курсовой работы (ККР) представляет собой завершающий этап изучения курса «Дополнительные главы математики».

Задачами ККР являются:

- закрепление и обобщение знаний, полученных студентами в процессе обучения;

- развитие навыков применения теоретических положений при решении практических инженерных задач по специальности;

- развитие навыков расчета, умение пользоваться технической и справочной литературой, ГОСТами;

- формирование инженерного мышления, подготовка к дипломному проектированию:

- развитие навыков в работах исследовательского характера;

- развитие навыков в работе с современными компьютерными технологиями.

2. ОСНОВНЫЕ ТРЕБОВАНИЯ К КОНТРОЛЬНО-КУРСОВОЙ РАБОТЕ

2.1 Тематика контрольно-курсовой работы

Темой задания ККР является нахождение линейных динамических моделей объектов управления по данным наблюдений за входом и выходом объекта, в частности, по разгонным характеристикам объектов и корреляционным функциям входо-выходных сигналов.

2.2 Исходные данные к контрольно-курсовой работе

Исходные данные к ККР выдаются преподавателем в виде номера варианта и приводятся в специальном разделе расчетно-пояснительной записки. В этом разделе указывается тема работы, номер варианта, данные разгонной характеристики и параметры корреляционных функций.

2.3 Объем контрольно-курсовой работы

Работа представляется к защите в виде расчетно-пояснительной записки объемом 10-15 листов формата 297×210 мм (ГОСТ 2.301-68). В записке приводятся все необходимые графические материалы на отдельных листах или миллиметровке. На отдельный графический лист можно вынести разгонную характеристику объекта с указанием на ней всех характерных точек, необходимых для поиска модели различными методами, а также автокорреляционную и взаимную корреляционную функции.

2.4 Выполнение контрольно-курсовой работы

График выполнения ККР доводится до студентов преподавателем и приводится в задании. На выполнение и защиту ККР отводится восемь недель. Контрольно-курсовая работа начинается с анализа задания и изучения настоящих указаний. В процессе работы студент пользуется консультациями и должен являться к руководителю на практические занятия. За неделю до срока окончания работы кафедра составляет, утверждает и доводит до сведения студентов график защиты ККР. За 3-4 дня до защиты студент представляет руководителю полностью оформленную пояснительную записку на проверку. Руководитель дает письменное заключение о качестве выполненной работы (рецензию), определяет возможность допуска студента, выполнявшего работу, к защите.

2.5 Защита контрольно-курсовой работы

При подготовке к защите студент анализирует заключение руководителя, вносит необходимые исправления и представляет повторно пояснительную записку на проверку с обязательным приложением предыдущей рецензии руководителя. Защита работы проводится перед комиссией в составе руководителя и членов комиссии, утвержденных решением кафедры. В докладе должна быть сформулирована задача, поставленная руководителем, освещены пути и методы ее решения, сравнение с существующими способами расчета, доказаны эффективность использования предлагаемых методов и моделей.

3. МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНО-КУРСОВОЙ РАБОТЫ

3.1 Содержание разделов пояснительной записки

Пояснительная записка к ККР должна содержать:

1. титульный лист;

2. задание на ККР;

3. содержание;

4. общетеоретическую часть;

5. расчетную часть;

6. заключение;

7. список используемых источников;

8. приложения.

3.2. Методические указания к выполнению отдельных разделов контрольно-курсовой работы

3.2.1. Титульный лист

Титульный лист выполняется по форме, приведенной в методических указаниях по оформлению технической документации, действующих на момент выполнения работы на кафедре.

3.2.2. Общетеоретическая часть

Должна содержать информацию о целях и задачах идентификации объектов управления, характеризовать типовые методы идентификации, содержать их сравнение.

3.2.3. Расчетная часть

Определение модели объекта по разгонной характеристике

В настоящее время при расчете настроек регуляторов локальных систем широко используются достаточно простые динамические модели промышленных объектов управления. В частности, использование моделей инерционных звеньев первого или второго порядка с запаздыванием для расчета настроек регуляторов обеспечивает в большинстве случаев достаточно качественную работу реальной системы управления.

В связи с этим одной из задач ККР является определения численных значений параметров динамических моделей по кривой разгона объекта управления.

В зависимости от вида переходной характеристики (кривой разгона) задаются чаще всего одним из двух видов передаточной функции объекта управления:

- в виде передаточной функции инерционного звена первого порядка с запаздыванием

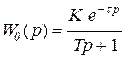, (3.1)

где - коэффициент усиления, постоянная времени и время запаздывания, которые должны быть определены в окрестности номинального режима работы объекта.

- в виде звена второго порядка с запаздыванием

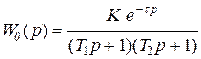. (3.2)

Перед началом обработки кривую разгона рекомендуется пронормировать (диапазон изменения нормированной кривой должен быть 0 - 1) и выделить из ее начального участка величину чистого временного запаздывания.

Динамический коэффициент усиления объекта определяется как отношение приращения выходного сигнала к приращению входного в окрестности рабочей точки. В нашем случае для всех вариантов заданий он очевидно равен единице.

Пример. Дана нормированная кривая разгона объекта, у которой заранее выделена величина чистого запаздывания . Построим по ее значениям, приведенным в табл. 3.1, график кривой разгона, показанный на рис. 3.1.

Таблица 3.1.

	0	2	4	6	8	10	12	14	18	22
	0	0,087	0,255	0,43	0,58	0,7	0,78	0,84	0,92	0,96

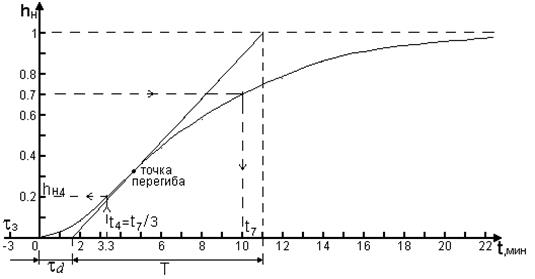
Рис. 3.1. График кривой разгона

Определение динамических характеристик объектов первого порядка с запаздываниеем по кривой разгона можно производить двумя методами.

1) Метод касательной к точке перегиба кривой разгона.

В данном случае точка перегиба соответствует переходу кривой от режима ускорения к режиму замедления темпа нарастания выходного сигнала. Постоянная времени Т и динамическое запаздывание определяются в соответствии с графиком, показанным на рис. 3.1, тогда .

2) Формульный метод позволяет аналитически вычислить величину динамического запаздывания и постоянной времени по формулам

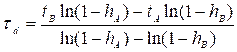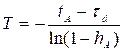, , (3.3)

где значение ,берется в окрестности точки перегиба кривой, а значение принимается равным 0,8. По этим значениям определяются моменты времени и .

Метод Орманса позволяет по нормированной кривой разгона определить две доминирующие постоянные времени объекта управления для модели.

Методика поясняется с использованием предыдущей кривой разгона, приведенной на рис. 3.1. Для этого по нормированной кривой разгона определяется время, соответствующее значению и обозначается . Полученный интервал делится на три части. Поднимается перпендикуляр до кривой разгона и определяется величина . Аналитически доказана связь между точками кривой разгона и параметрами модели, а именно

Постоянные времени объекта управления и определяются с помощью вспомогательной величины , для нахождения которой используется номограмма, приведенная на рис. 3.2.

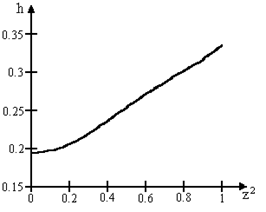
Рис. 3.2. Номограмма для определения величины

Постоянные времени объекта управления и определяются по следующим формулам:

(3.4)

Если , то для определения динамики объекта используют метод площадей.

Типовые табличные методы корреляционной идентификации

Как известно корреляционные методы идентификации основаны на решении интегрального уравнения Винера–Хопфа

. (3.5)

Одним из самых простых и эффективных способов решения этого уравнения является табличный метод типовой идентификации, разработанный под руководством проф. Райбмана Н. С. [3]. Идея метода чрезвычайно проста: были заданы несколько типичных автокорреляционных функций входных сигналов объекта Ruu(t), работающего в нормальном режиме, и по ним, последовательно задаваясь различными характеристиками типовых динамических объектов, а именно дифференциальными уравнениями до 3-го порядка включительно, были построены соответствующие взаимно корреляционные функции входного и выходного сигналов. Таким образом, была получена достаточно обширная таблица соответствия между корреляционными функциями Ruu(t), Ryn(t) и моделями объектов, заданными в виде дифференциальных уравнений с известными параметрами, охватывающими достаточно обширный класс реальных объектов, названных типовыми [3].

В результате, процесс идентификации сводится, по существу, к нахождению оценок корреляционных функций и по экспериментально полученным входо-выходным выборкам и правильному использованию имеющейся таблицы. Аппроксимация экспериментально полученных оценок и табличными функциями будет приводить к некоторой погрешности в определении модели объекта, однако во многих практических случаях эта погрешность оказывается вполне приемлемой особенно с учётом минимальности затрат усилий и времени при такой идентификации.

Правила использования таблиц типовой идентификации

1. Таблицы построены для трёх основных типов автокорреляционных функций входного сигнала:

1). (графики 2-х подтипов приведены на рис. 3.1.1 и 3.1.7 в книге [3]);

2). (рис. 3.3.1 и 3.3.21 в книге [3]);

(рис. 3.5.1 в книге [3]).

Поэтому сначала по внешнему виду экспериментально полученной оценки автокорреляционной функции выбираются соответствующие таблицы. Например, если по внешнему виду похожа на автокорреляционную функцию первого типа, то выбираются таблицы 3.1 и 3.2, если второго, то 3.3 и 3.4, если третьего, то 3.5 и 3.6 согласно книге [3].

2. Далее по выбранной из соответствующей таблицы и экспериментальной автокорреляционным функциям определяется масштабный коэффициент k по оси времени, получаемый из соотношения , где с – масштабный коэффициент по оси ординат.

3. Строится промежуточная взаимно корреляционная функция выходной и входной переменных по экспериментально полученной взаимно корреляционной функции согласно:

. (3.6)

4. Для облегчения поиска табличной взаимно корреляционной функции, наиболее близкой по форме к , таблица в книге [3] всех возможных взаимно корреляционных функций разбита на группы похожих по форме кривых и построена специальная таблица типичных групповых взаимно корреляционных функций. По этой таблице сначала определяется номер наиболее близкой по форме группы функций, и затем поиск кривой ведётся в уже выбранной группе. В результате, достаточно быстро и просто оказывается выбрана табличная взаимно корреляционная функция , наиболее близкая по форме к , а по ней уже определяется табличное дифференциальное уравнение с известными табличными коэффициентами, например, третьего порядка

. (3.7)

5. Вычисляется масштабный коэффициент k3 по формуле:

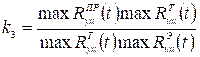. (3.8)

6. Коэффициенты дифференциального уравнения, найденные по таблице в пункте 4, для учета разницы масштабов корреляционных функций пересчитываются по формулам:

3-й порядок:

2-й порядок:

1-й порядок:

Пример решения задачи:

Необходимо определить оператор цементной мельницы Серебряковского цементного завода (размер мельницы 2,6х13 м). В качестве входного сигнала цементной мельницы рассматривается положение ножа тарельчатого питателя клинкером - ; в качестве выходного сигнала – тонкость помола - . Заданы автокорреляционная и взаимно корреляционная функции входного и выходного сигналов, вычисленные по их экспериментально снятым реализациям, показанные на рис. 3.3.

Определим оператор данного объекта по изложенному выше алгоритму с использованием таблиц из книги [3].

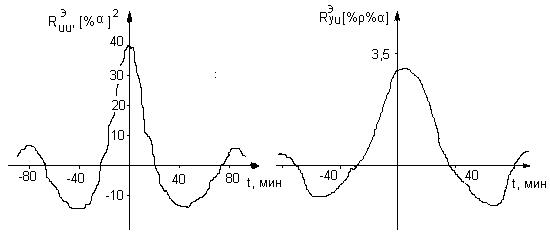
Рис. 3.3.

1. Для кривой из таблиц в книге [3] определяем наиболее близкую к ней по форме автокорреляционную функцию (рис. 3.3.21 [3]), аналитически выражаемую следующим образом:

.

2. Определяем масштабный коэффициент k:

с/мин,

где и - отрезки оси времени на графиках кривых и соответственно от нуля до первого пересечения кривыми оси времени.

3. Строим промежуточную кривую

.

Отметим, что по внешнему виду она будет совпадать с кривой , однако будет иметь другие масштабы по осям абсцисс и ординат.

4. По таблицам 3.3 и 3.4 из книги [3] определяется , как табличная взаимно корреляционная функция, наиболее близкая по форме к кривой (или ). В данном примере это будет кривая, изображенная на рис. 3.4.6 в книге [3], соответствующая объекту первого порядка с коэффициентами: с-1; с-1.

5. Вычислим масштабный коэффициент

.

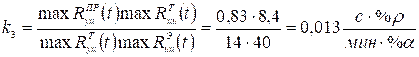6. Пересчитаем коэффициенты дифференциального уравнения

;

.

Таким образом, окончательно идентифицированный объект описывается дифференциальным уравнением

или передаточной функцией

.

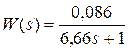3.2.4. Заключение

Должно содержать основные выводы по работе.

4. МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ПРОВЕДЕНИЮ ИНДИВИДУАЛЬНОЙ РАБОТЫ

На выполнение ККР отводится 5 часов самостоятельных занятий студентов. Тематика занятий должна соответствовать ходу выполнения работы. Целью занятий является закрепление теоретического материала, приобретение практических навыков в расчете параметров линейных динамических моделей объектов управления, обеспечивающих своевременное выполнение ККР. Самостоятельные занятия студентов сопровождаются индивидуальными консультациями преподавателя.

Проведение индивидуальных консультаций начинается с анализа темы ККР, уяснения общих задач, стоящих перед студентами, уточнения отдельных практических вопросов. Однако, в любом случае основную часть ККР должна составлять самостоятельная работа студентов при активном участии в этом процессе руководителя.

Библиографический список рекомендуемой литературы

1. Кочетыгов А. А. Методы идентификации: Учеб. пособие. – Тула: Изд-во ТулГУ, 2001. – 220 с.

2. Гроп Д. Методы идентификации систем. - М.: Мир, 1979. - 302 с.

3. Типовые линейные модели объектов управления / Под ред. Н. С. Райбмана. - М.: Энергоатомиздат, 1983. - 264 с.

4. Лившиц К. И. Идентификация: Учеб. пособие. - Томск: Изд-во ТГУ, 1981. - 132 с.

5. Льюнг Л. Идентификация систем. Теория для пользователя. - М.: Наука, 1991. - 432 с.

6. Эйкхофф П. Основы идентификации систем управления. Оценивание параметров и состояния. - М.: Мир, 1975. - 686 с.

7. Ройтенберг Я. Н. Автоматическое управление: Учеб. Пособие. – М.: Наука, 1992. – 576 с.

8. Коновалов В. И. Идентификация объектов управления: Учеб. пособие. - Томск: Изд-во ТПУ, 1981. - 90 с.

9. Кухаренко Н. В. Математические модели объектов управления и их статистическая идентификация: Учеб. пособие. – Л.: 1982. – 87 с.

10. Методы классической и современной теории автоматического управления: Учебник в 3-х т. Т.1: Анализ и статистическая динамика систем автоматического управления / Под ред. Н. Д. Егупова. - М.: Изд-во МГТУ им. Н. Э. Баумана, 2000. – 748 с.

Скачать полный текст - Дополнительные главы математики.zip